2018-12-19

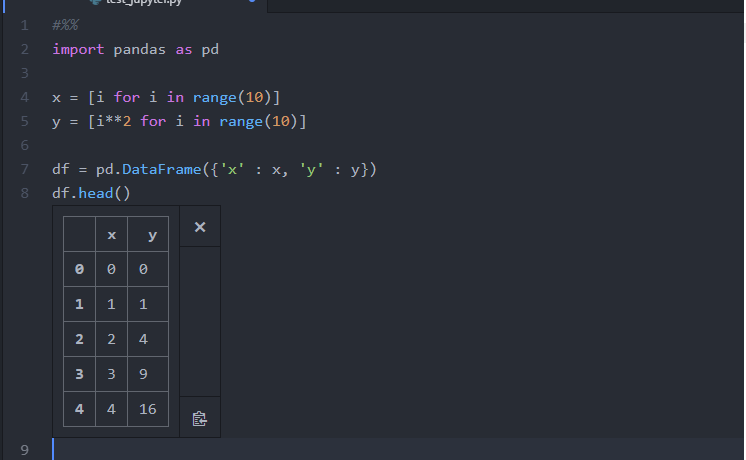
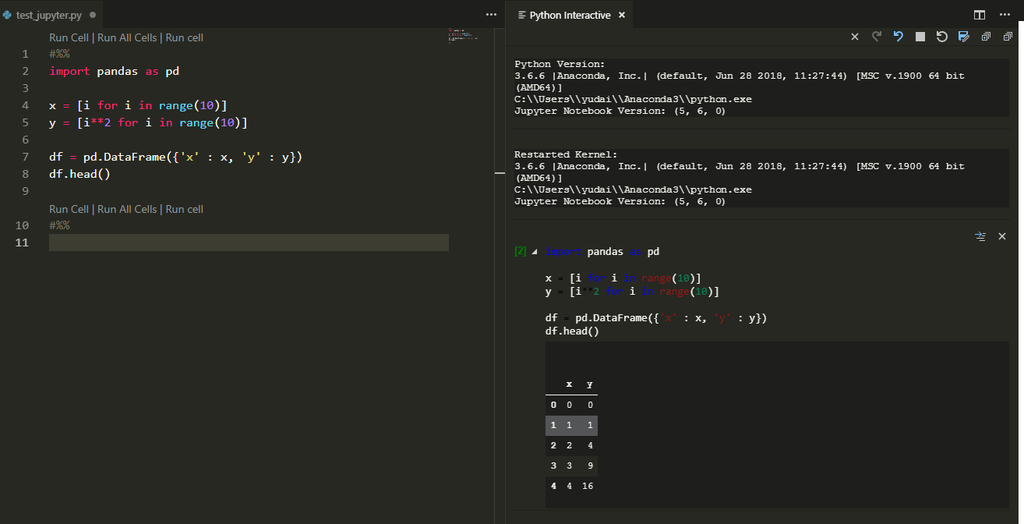
AtomとVSCodeのJupyter Notebook環境を比較した

仕事でよくJupyter Notebookを使ってのデータ解析を行うのですが、最近いちいちブラウザでNotebookを起動するのが面倒になってきました。そこでエディタを使ってJupyter Notebookを使おうと思って色々調べていたら、AtomとVSCodeを使うのがどうやらよさそうだということがわかりました。

そこで、この記事では、両方の環境を使ってみてどちらがより使いやすいか比較してみたいと思います。

開発環境
環境構築
- エディタをインストールする
- Python環境を整える
Jupyter Notebookを使う環境を整えていく
- Atomの場合
- VSCodeの場合
使ってみる
まとめ

開発環境

Windows10
Python 3.6.5 (Anaconda)
Atom 1.33.0
VSCode 1.29.1

環境構築

PythonとJupyter Notebookを使いたい場合には、Anacondaで入れてしまうのが一番簡単です(特にWindowsでは)。
weblabo.oscasierra.net

エディタをインストールする

AtomやVSCodeのインストール方法は下のリンクからダウンロード、インストールするだけです。
atom.io
code.visualstudio.com

Python環境を整える

次に各エディタにPythonの環境を整えていきます。
Atomの場合：
https://hajipro.com/python/atom-python

VSCodeの場合：
docs.microsoft.com

手順はAtomのほうが圧倒的に楽です。

Jupyter Notebookを使う環境を整えていく

Atomの場合

AtomではFile -> Settingsを押すと、
f:id:pyhaya:20181202173420p:plain
という画面が出てきます。左側の列にCoreやらEditorやらいろいろ並んでいますが、一番下のInstallを選択し出てくる検索欄に「Hydrogen」と入れて検索します。後は出てきたHydrogenをインストールするだけです。

VSCodeの場合

こちらもAtomと似たような感じです。
f:id:pyhaya:20181202173854p:plain
VSCodeの場合には常に画面の一番左側にアイコンが5つ並んでいます。一番下の四角いやつがパッケージのインストールなどに使うものです。
このアイコンを押して、「Jupyter」と検索し、一番上に出てくるJupyterパッケージをインストールします。

使ってみる

いよいよ使ってみます。どちらのほうが使い勝手が良いでしょうか？

普通に使ってみる

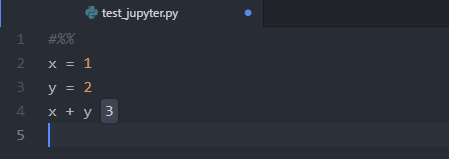
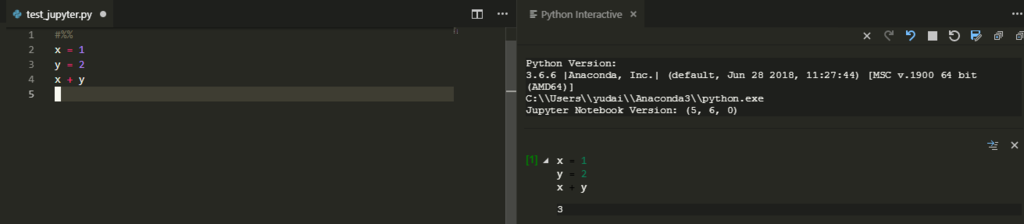
まずは普通に、算術計算に使ってみます。次のコードを実行してみます。

x = 1
y = 2
x + y

両方ともコードブロックはブロックの先頭に#%%を入れることで表現できます。

Atom

f:id:pyhaya:20181202175025p:plain
Atomの場合はこんな感じ。ブロックの実行はAlt-Shift-Enterでできます。Shift-Enterだと一行ずつ実行になります。

VSCode

VSCodeの場合はこんな感じ。Shift-Enterで実行できます。Atomとは異なり画面分割されて出力されます。表示はこちらのほうがJupyter Notebookに近い印象です。
f:id:pyhaya:20181202175301p:plain

グラフを書く

下のコードを実行してみます。

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 10, 500)
y = np.sin(x)

plt.figure()
plt.plot(x, y)
plt.show()

Atom

f:id:pyhaya:20181202175919p:plain
きれいに出力されました。

VSCode

f:id:pyhaya:20181202180144p:plain

こちらもきれいに、、、とは言ってません。軸のラベルが背景の黒につぶされてしまっています。これをどうにかするには

plt.figure(facecolor='white')

と色を指定してやる必要があります。このめんどくささがあるので、描画に関してはAtomに軍配が上がりそうです。

CSVファイルを扱う

Atom

f:id:pyhaya:20181202180934p:plain
かなりシンプルな感じで出力されます。

VSCode

f:id:pyhaya:20181202181035p:plain
わかりにくいですが、行ごとに色が若干違っています。また、Atomとは異なり表にカーソルを持っていくと行がハイライトされます。この点はAtomより優れています。

まとめ

AtomもVSCodeもよく使うようなJupyter Notebookの機能はちゃんと備わっているという感じです。ただ、細かいところで両者とも使いにくいところがありました。上には書きませんでしたが、VSCodeではos.chdir()をしてもセルが変わるとルートディレクトリに戻されるという謎の現象もありました。

どの機能を重要視するかによってどちらを選ぶかは変わりそうですが、私の場合は、グラフの色調整は結構気合い入れてやることが多いので、いちいち色指定しなくてよいAtomかなって感じです。

2018-12-07

機械学習を原理から理解する　回帰

Python 機械学習プログラミング

機械学習をただ使うだけでなく、どのような原理で動いているのか理解するために数学的な観点からちゃんとアルゴリズムを見てみます。

前回は線形回帰の記事を書きました。
pyhaya.hatenablog.com

今回は、前回の線形回帰のアルゴリズムを拡張して、高次の回帰をしていきます。

前回の復習（線形回帰）
高次多項式での回帰

前回の復習（線形回帰）

前回はデータ点を直線で回帰するために、最小二乗法を使った方法について説明しました。ここでは回帰直線を

$y = \mathbf{w}\cdot\mathbf{x} \tag{1}$

というように重みパラメータ $\mathbf{w}$ とデータ $\mathbf{x}$ の内積で表現しました。そして、適切な重みを見つけるための指針として正解 $t$ との二乗誤差

$\displaystyle \sum_{i=1}^n(y_i-t_i)^2 \tag{2}$

を最小にしようということになり、行列計算によってこのような重みパラメータを得られることを見ました。

高次多項式での回帰

前回の記事だけでも、複数の特徴量の線形和の形での回帰は可能です。今回はさらにバリエーションを増やすために高次多項式での回帰を行います。つまり、回帰曲線は下のような式であらわされます。

$y = w_1x + w_2x^2+w_3x^3+\cdots \tag{3}$

見やすさのため変数は1つのものを書いています。また、いつも通りバイアスは重みパラメータ内部に入れています。

理論

実は、理論的にはこの回帰は線形回帰と同一の方法で実行することができます。というのも、(3)式はベクトルの形式で書き直すと

$y = \mathbf{w}\cdot\mathbf{\phi}(x) \tag{4}$

ここで $\phi$ は

$\mathbf{\phi(x)} = (x, x^2, x^3,\cdots, 1)^T \tag{5}$
です。最後の1はバイアスを重みパラメータの中に取り込んだために出てきた項です。この形は線形回帰でやったものと全く同じです。なので同じアルゴリズムで解くことができます。

$A\mathbf{w}=b,\ \ \ \ \ \displaystyle (A =\sum_{i=1}^n \mathbf{\phi_i}\mathbf{phi_i}^T,\ \ \mathbf{b}=\sum_{i=1}^n y_i\mathbf{x_i}) \tag{6}$

添え字 $i$ は訓練データの番号です。

実装(Python3)

上の理論を見ながらPythonで実装を行ってみます。

import matplotlib.pyplot as plt
import numpy as np

from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression

def Regression(X, y, dim):
    d = X.shape[1] + 1
    A = np.zeros((d+dim-1, d+dim-1))
    b = np.zeros((d+dim-1, 1))

    for i in range(len(X)):
        x = [] 
        for j in range(1, dim+1):
            x += list(X[i]**j)
        x.append(1)
        x = np.array(x).reshape((d+dim-1, 1))
        A += x.dot(x.T)
        b += y[i] * x

    return np.linalg.inv(A).dot(b)

if __name__ == "__main__":
    X, y = make_regression(
        n_samples=50,
        n_features=1,
        noise=4,
        random_state=42
    )

    dim = 2    #何次の多項式で回帰を行うか
    pred = Regression(X, y, dim)
    x = np.linspace(-2, 1.9, 50)
    y_pred = np.zeros_like(x)
    for i in range(0, dim):
        y_pred += pred[i][0] * x**(i+1)
    y_pred += pred[dim][0]
  
    plt.figure()
    plt.plot(X, y, 'o')
    plt.plot(x, y_pred)
    plt.show()

回帰結果を見てみる

回帰結果を次数を変えてみてみます。まずは二次の場合フィッティング結果は下のようになります。
f:id:pyhaya:20181207075342p:plain

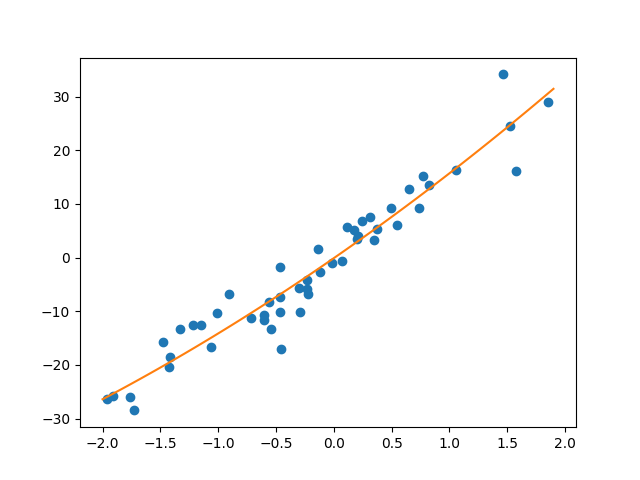
回帰はうまくいっている印象です。次に次数を増やしてみます。十次のとき
f:id:pyhaya:20181207075443p:plain

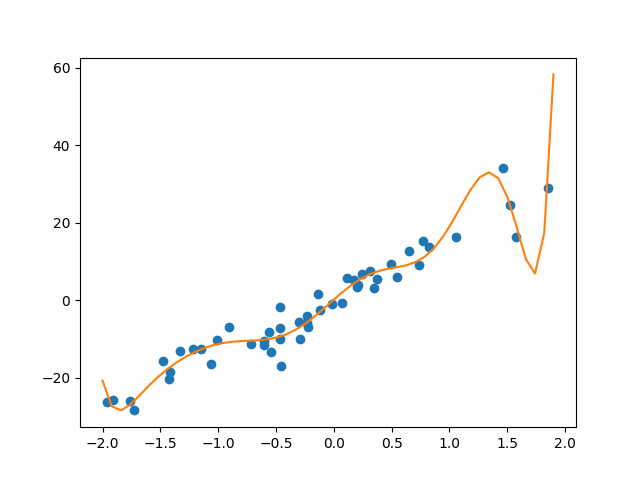
明らかにノイズも拾って回帰してしまっています。これは訓練データを過度に学習してしまっている状況で、過学習状態となっています。

2018-12-01

機械学習を原理から理解する　線形回帰

最近始めた機械学習の理論的な話の３つめです。相変わらず線形の話が続きます。過去記事を下に貼っておきます。

pyhaya.hatenablog.com
pyhaya.hatenablog.com

今回は、前回までの分類アルゴリズムとは異なり、回帰アルゴリズムについて書きます。

回帰とは
線形回帰
回帰直線を求める
Pythonで書く
逆行列が存在しないとき

回帰とは

回帰というのは、データセットがあったときにパラメータと目的変数の間に成り立つ関係式を見つける操作です。実験とかで結果を理論曲線でフィッティングするイメージです。

...もう少し具体的な例を出すと、例えば、パラメータとして、過去1カ月分の降水量と気温、天候が与えられたときにある特定の日に収穫されたリンゴの糖度（目的変数）を予測するとかなると回帰を使います。降水量、気温、天候というデータを組み合わせることでリンゴの糖度を表現するわけです。

線形回帰

線形という表現からもわかるように、回帰の式に一次関数を使うのが線形回帰です。例えばパラメータが1つあって(xと書く)、そこからある変数の値(yと書く)を予測したいとします。いま、学習のためにいくつかデータが与えられていて、下のグラフのように分布しているとします。
f:id:pyhaya:20181129000333p:plain
これはおおむね線形に分布していることがわかります。これを一変数の一次関数で回帰したのがオレンジの直線になります。

回帰直線を求める

パラメータ

線形回帰をする際に求める必要があるのは次の2種類のパラメータです。一つは重みパラメータ $\mathbf{w}$ そしてもう一つがバイアス $b$ です。回帰に使うパラメータが1種類の時には重みパラメータは2次元平面上の直線の傾きを表します。

$h(\mathbf{x}) = \mathbf{w}\cdot\mathbf{x}+b \tag{1}$

ここで $\mathbf{x}$ は与えられている学習データで、 $h(\mathbf{x})$ がそのデータから計算した目的変数の予測値です。ふつうは、バイアスも重みパラメータの中に取り込んだ下のような形を使います。

$h(\mathbf{x}) = \mathbf{w}\cdot\mathbf{x} \tag{2}$

ここで $\mathbf{w}=(w_1, w_2,\cdots, b)$ , $\mathbf{x}=(x_1, x_2,\cdots, 1)$

損失関数

回帰の際には、どれくらいうまく回帰ができているかを知るために損失関数を定義します。回帰によってこの損失関数を最小化することが目標になります。

線形回帰の際によく用いられる損失関数は二乗誤差です。二乗誤差は下のように定義されます。

$\displaystyle L_S(h)=\frac{1}{n}\sum_{i=1}^n(h(\mathbf{x_i})-y_i)^2 \tag{3}$

$n$ は学習データの数です。

損失関数を最小化する

損失関数をなるべく小さくするにはどのようにすればよいでしょうか？微分して0になる値を探します。

$\displaystyle \frac{d}{d\mathbf{x}}L_S(h)=\frac{2}{n}\sum_{i=1}^n(\mathbf{w}\cdot\mathbf{x_i}-y_i)\mathbf{x_i} =0 \tag{4}$

ここで、２つ変数を導入します。

$\displaystyle A =\sum_{i=1}^n \mathbf{x_i}\mathbf{x_i}^T,\ \ \mathbf{b}=\sum_{i=1}^n y_i\mathbf{x_i} \tag{5}$

$A$ は行列です。これを使うと、(4)式は下のように簡単に書くことができます。

$A\mathbf{w}=\mathbf{b} \tag{6}$

つまり、パラメータは $A$ の逆行列が求まれば、

$\mathbf{w}=A^{-1}\mathbf{b}\tag{7}$

と求めることができます。

Pythonで書く

上の計算をPythonのコードに書き下すと下のようになります。

import matplotlib.pyplot as plt
import numpy as np

from sklearn.model_selection import train_test_split
from sklearn.datasets import make_regression


def LinearRegression(X, y):
    A = np.zeros((X.shape[1]+1, X.shape[1] + 1))
    b = np.zeros((X.shape[1]+1, 1))
    for i in range(len(X)):
        x = list(X[i])
        x.append(1)
        x = np.array(x).reshape((2, 1))
        A += x.dot(x.T)
        b += y[i] * x

    return np.linalg.inv(A).dot(b)


if __name__ == '__main__':
    X, y = make_regression(
        n_samples=50,
        n_features=1,
        noise=7,
    )

    w = LinearRegression(X, y)
    fit_x = np.linspace(-2, 2, 500)
    fit_y = fit_x * w[0, 0] + w[1, 0]
    plt.figure()
    plt.plot(X, y, 'o')
    plt.plot(fit_x, fit_y)
    plt.show()

9, 10行目でX.shape[1]+1のように+1しているのは、バイアスを重みパラメータの中に取り込むために、配列の要素数を1つ増やすためです。

このコードでは、簡単のために変数は1種類にしています。そのため計算結果は簡単に図示することができて、
f:id:pyhaya:20181129011247p:plain
うまくいっていることが見て取れます。

逆行列が存在しないとき

ここからは、少しだけ発展的な内容になります。

このアルゴリズムでは、計算に逆行列を使っています。しかし、逆行列は必ずしも存在するとは限りません。このようなときにはどのように計算すればよいか考えます。

逆行列が存在しないときというのは、線形代数の知識を使えば固有値に0を含むときであることがわかります。このようなときに行列Aを

$A = VDV^\dagger \tag{8}$

のように直交行列 $V$ と固有値を対角成分にもつ対角行列 $D$ を使って分解することができます。 $D$ の対角成分に0が含まれなければ、Dのすべて対角成分をすべて逆数にした行列 $D^+$ がDの逆行列になり、実際、

$VDV^\dagger VD^+V^\dagger=VDD^+V\dagger=VV^\dagger=1 \tag{9}$

のように、真ん中から次々に単位行列に代わっていきます(直交行列 $V$ は転置して複素共役をとった $V^\dagger$ と掛けると単位行列になる性質を利用しています。 Wiki参照)。

対角成分に0が含まれていては、このような操作は行うことができません。この時には $D^+$ を次のように定義します。

$D^+_{ii} = \begin{cases}1/D_{ii}\ \ \ \ (D_{ii}\neq 0)\\ 0 \ \ \ \ (\mathrm{else})\end{cases} \tag{10}$

要するに、逆数とれるならとって、とれないなら0のままにしておくということです。このような $D^+$ によって計算される $A$ を

$A^+=VD^+V^\dagger \tag{11}$

として逆行列の代わりに使えば、

$\displaystyle A\mathbf{w}=A(A^+\mathbf{b})=VDV^\dagger(VD^+V^\dagger)\mathbf{b} = \sum_{i:D_{ii}\neq0} \mathbf{v}_i\mathbf{v}_i^T\mathbf{b} \tag{12}$

となります。 $A\mathbf{v}$ は $V$ 中の列ベクトルです。最右辺を見てみると、 $A\mathbf{w}$ が $D_{ii}\neq 0$ であるような $i$ についての $\mathbf{v}_i$ によって張られる空間への射影になっていることがわかります。このように空間を制限して考え直すことで、逆行列が存在しない場合においても回帰計算をすることが可能になります。

2018-11-27

機械学習を原理から理解する　パーセプトロン

内容的には、前回の記事の続き的な感じになります。
pyhaya.hatenablog.com

今回は、二値分類をパーセプトロンを使って実装します。パーセプトロンといえば、ニューラルネットワークやディープラーニングの基本という感じの学習器です。前回に引き続き、理論を説明した後にPythonでの実装を示します。

対象とする問題
学習アルゴリズム
どのように解くか
Pythonでの実装

対象とする問題

いくつかの特徴量が与えられていて、それに対して正解ラベルが+1, -1で与えられているような状況を考えます。考える仮説空間はhalf-spacesクラス（日本語訳がわからない）です。

仮説空間という言葉が出てくると難しく感じますが、予測に使うのは下のような関数です。

$y = sign(\mathbf{w}\cdot\mathbf{x} + b)\tag{1}$

$\mathbf{w}, b$ は重みとバイアスです。基本的には線形関数で、最終的にsignで符号だけ取り出すことで予測値 $y$ を算出しています。

学習アルゴリズム

これは前回の記事と同じなので結果のみ示します。最終的には、

$t_i(\mathbf{w}\cdot\mathbf{x}_i) > 0 \tag{2}$

を満たす重みパラメータ $\mathbf{w}$ を求めることが目標になります。

どのように解くか

前回の記事では、これを線形計画問題だと考えて解きました。今回は、線形計画に比べると直感的な方法でパラメータを求めていきます。

まず、パラメータ $\mathbf{w}$ を $t_1\mathbf{x}_1$ で初期化します。なぜこのような値で初期化するかというと、こうすることで

$t_1(\mathbf{w}\cdot\mathbf{x}_1)=t_1^2x_1^2 > 0 \tag{3}$

となって、ひとまず最初のデータに関して学習させることができるためです。

次にやることは $\mathbf{w}$ はこれで最適か調べることです。学習データを(2)式に代入していって、不等式が成り立っているか確かめます。すべての学習データで不等式が成立していればこのパラメータが最適値とすることができます。しかしほとんどの場合はこううまくはいきません。 $i$ 番目のデータで

$t_i(\mathbf{w}\cdot\mathbf{x}_i) \le 0 \tag{4}$

となってしまった場合を考えましょう。どうすればよいでしょう。要するに、左辺を増やす方向に $\mathbf{w}$ を更新すればよいです。どうやるかというと、

$\mathbf{w}\rightarrow \mathbf{w}+y_i\mathbf{x}_i\tag{5}$

このとき、(4)式の左辺は

$t_i(\mathbf{w}\cdot\mathbf{x}_i) \rightarrow t_i(\mathbf{w}\cdot\mathbf{x}_i)+\| \mathbf{x}_i\|^2\tag{6}$

となります。ここで、正解ラベル $t_i$ は±1しかとらないことを使いました。無事左辺を増やせました。このようにして、すべての学習データについて(2)式が成り立つまで値の更新を続けます。

Pythonでの実装

値の更新は、現実問題としてすべての学習データを間違えることなく予測することは不可能なことが多いので、適当なところで打ち切ります。100回の値更新で打ち切るようにしたのが下のプログラムです。

import numpy as np

from sklearn.model_selection import train_test_split
from sklearn.datasets import make_classification

def Perceptron(X, y):
	X = np.array(X)
	w = np.zeros(len(X[0]))
	w = y[0] * X[0]

	for count in range(100):
		success = True
		for i in range(len(X)):
			if np.sign(w.dot(X[i])) == np.sign(y[i]):
				continue
			else:
				w += y[i]*X[i]
				success = False
				break
		if success:
			break
	
	return w

if __name__ == '__main__':
	#サンプル生成
	X, y = make_classification(
			n_samples=500,
			n_classes=2,
			n_features=2,
			n_redundant=0,
			class_sep=1.5,
			)

	y = list(map(lambda x: -1 if x == 0 else 1, y))
	X = np.array(X)
	y = np.array(y)
	X_train, X_test, y_train, y_test = train_test_split(X, y)

	w = Perceptron(X_train, y_train)
	accuracy = np.sum(y_test*X_test.dot(w) > 0)
	print(accuracy / len(X_test))

これを実行すると、だいたい95%程度の精度が出ていることが確認できます。

2018-11-26

Kaggleのタイタニックデータの解析

Kaggle Python データサイエンスプログラミング

Kaggleの定番データセットといえば「タイタニックの生存者予測」です。今回は生存者の予測を目指して解析を行っていきたいと思います。データの可視化について詳しい説明は前回記事で書いているのでそちらを参照してください。
Titanic: Machine Learning from Disaster | Kaggle

解析環境
データの全体像の把握
- 変数の吟味
- カテゴリ変数を数値へ変換していく
Ticketを処理する
ここまでの処理の結果

解析環境

Kaggleのカーネル

データの全体像の把握

データ解析をする際に最も重要なことはもちろんデータを理解することです。まずは大雑把にデータの全体像を見てみましょう。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

import os
import warnings
warnings.filterwarnings('ignore')
print(os.listdir("../input"))

# -> ['train.csv', 'gender_submission.csv', 'test.csv']

train = pd.read_csv('../input/train.csv')
test = pd.read_csv('../input/test.csv')
train.head()

f:id:pyhaya:20181118104522p:plain

いくつかの変数があることがわかります。

PassengerId : 乗客ID
Survived : 生存ラベル(1: 生存 0:死亡)
Pclass : 身分(1が最高)
Name : 乗客氏名
Sex : 性別
Age : 年齢
SibSp : 乗客中の親戚の人数
Parch : 乗客中の親もしくは子供の人数
Ticket : チケット番号
Fare : 乗船料
Cabin : 客室番号
Embarked : どこの港で乗船したか

変数の吟味

これらの変数の中で、中心となるのはもちろん'Survived'です。これにほかの変数が影響を与えうるか考えてみます。

'PassengerId', 'Ticket'

'PassengerId'はただの通し番号なので、生存には関係ない気がします。ただ、これが乗客の身分や部屋の位置に関係する可能性は一度調べる必要がありそうです。これは'Ticket'にも言えます。

'Pclass', 'Cabin', 'Fare'

'Pclass'に関しては、漠然と、身分の高い人は安全なところに客室があるのかなと思うので、関係ありそうです。これも後で解析しましょう。同様に'Cabin'と'Fare'も調べてみます。

'Sex', 'Age'

'Sex'や'Age'に関しては、欧米ではレディーファーストの精神が強いので女性や子供が優先的に救助されていた可能性があります。

'Name'

'Name'は生存とは全く関係なさそうに見えます。ただ、上の表を見てみると、乗客の名前には最初に'Mr'や'Mrs'などがついていることがわかります。これはその人の社会的な地位や状態を表しているといえるので、ここの情報だけは使える気がします。

'SibSp', 'Parch'

これらは親戚関係のパラメータですが、正直、これらのパラメータが'Survived'に効いてくるストーリーは思いつきませんでした。相関係数だけ調べて、早々に落としてもいいかもしれません。

'Embarked'

乗船地です。これはその土地の発展状況によって乗客層の経済力を示している可能性があります。

カテゴリ変数を数値へ変換していく

'Name'を変換する

'Name'の変換は少し手間です。まずは正規表現を使って敬称を取り出し、'Title'という名前の新しいカラムを作ります。

train['Title'] = train['Name'].str.extract(r'([A-Za-z]+)\.', expand=False)
test['Title'] = test['Name'].str.extract(r'([A-Za-z]+)\.', expand=False)

数値に置き換える

では、'Sex', 'Embarked', 'Title'を数値に変換していきます。これにはsklearn.preprocessing.LabelEncoderを使います。

from sklearn.preprocessing import LabelEncoder

for col in ['Sex', 'Title']:
    le = LabelEncoder()
    le.fit(train[col])
    train[col] = le.transform(train[col])
    
    le.fit(test[col])
    test[col] = le.transform(test[col])


train['Embarked'] = train['Embarked'].map({'S' : 1, 'C' : 2, 'Q' : 3})
test['Embarked'] = train['Embarked'].map({'S' : 1, 'C' : 2, 'Q' : 3})

多分'Embarked'はnull valueがあってうまくいかなかったので普通にmapを使って置き換えました。

'Name'を落とす

もう名前情報はいらなくなったので落としてしまいましょう。

train.drop('Name', axis=1, inplace=True)
test.drop('Name', axis=1, inplace=True)

ここまでやってきて、データの状況は下のようになっています。
f:id:pyhaya:20181118181123p:plain

Ticketを処理する

現時点ではまだ、'Ticket'が数値量になっていません。しかし、どのように数値に変換してよいのかはっきりしないので、もう少し詳しくこの変数について知ることにします。

いくつかTicketを眺めてみると、数字だけからなるチケット番号と、アルファベットが混ざるものの2つがあることがわかります。まずはこれから分離してみます。

number_ticket = train[train['Ticket'].str.match('\d+')]
num_alpha_ticket = train[train['Ticket'].str.match('[A-Z]+.+')]

数字だけのチケット

数字だけのチケットnumber_ticketについてまず見てみましょう。数字がどんなふうに分布しているか見るために、簡単なプロットをしてみます。

number_ticket['Ticket'] = number_ticket['Ticket'].apply(lambda x: int(x))
number_ticket.sort_values('Ticket', inplace=True)

plt.figure()
plt.plot(number_ticket['Ticket'], '-o')
plt.show()

f:id:pyhaya:20181118192749p:plain

大きく分けて2つのグループに分かれている様子が見て取れます。ylimをいじって拡大してみると、チケット番号は以下の5通りに分けられることがわかります。

10000以下
i*1e+4より大きく(i+1)*1e+4以下 (i=1,2,3)
300000以上

このグループ分けをしたときに、生存率に差が出るか見てみましょう。

x = [1, 2, 3, 4, 5]

lowest_num_ticket = number_ticket[number_ticket['Ticket'] <= 100000]
sec_lowest_num_ticket = number_ticket[(number_ticket['Ticket'] > 100000) & (number_ticket['Ticket'] < 200000)]
thir_lowest_num_ticket = number_ticket[(number_ticket['Ticket'] > 200000) & (number_ticket['Ticket'] < 300000)]
four_lowest_num_ticket = number_ticket[(number_ticket['Ticket'] > 300000) & (number_ticket['Ticket'] < 400000)]
high_num_ticket = number_ticket[number_ticket['Ticket'] > 3000000]
y = [lowest_num_ticket['Survived'].mean(), sec_lowest_num_ticket['Survived'].mean(),
     thir_lowest_num_ticket['Survived'].mean(), four_lowest_num_ticket['Survived'].mean(),
     high_num_ticket['Survived'].mean()
    ]

plt.figure()
plt.bar(x, y)
plt.xlabel('ticket number')
plt.ylabel('Survived')
plt.show()

f:id:pyhaya:20181118194155p:plain

数字が大きいほど生存率が小さくなるという傾向がありそうです。

アルファベットが入ったチケット

こちらは上に比べて分類が面倒です。正規表現を使ってうまくやっていきます。

A_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('A.+')]
CA_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('C\.*A\.*.+')]
PC_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('PC.+')]
PP_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('PP.+')]
SOTON_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('SOTON.+')]
STON_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('STON.+')]
LINE_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('LINE.*')]
FC_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('F\.C\.(C\.)*.+')]
W_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('W.+')]
C_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('C.+')]
SC_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('S(\.)*C.+')]
SO_ticket = num_alpha_ticket[num_alpha_ticket['Ticket'].str.match('S(\.)*O.+')]
other_ticket = num_alpha_ticket[
    num_alpha_ticket['Ticket'].str.match(
        '(Fa)*(P/PP)*(S\.P)*(S\.*W)*.+'
    )
]

x = [i for i in range(1, 14)]
y = [A_ticket['Survived'].mean(), CA_ticket['Survived'].mean(), PC_ticket['Survived'].mean()
    ,PP_ticket['Survived'].mean(), SOTON_ticket['Survived'].mean(), STON_ticket['Survived'].mean()
    ,LINE_ticket['Survived'].mean(), FC_ticket['Survived'].mean(), W_ticket['Survived'].mean()
    ,C_ticket['Survived'].mean(), SC_ticket['Survived'].mean(), SO_ticket['Survived'].mean()
    ,other_ticket['Survived'].mean()
    ]

plt.figure()
plt.bar(x, y)
plt.ylabel('survived')
plt.show()

f:id:pyhaya:20181118194601p:plain

このように場合分けが多岐にわたるときには、漏れがないか確認する手段を持っておくことが重要です。今回の場合は、セット型を使ってチェックが可能です。

new_set = set(A_ticket['Ticket']) | set(CA_ticket['Ticket']) |\
        set(PC_ticket['Ticket']) | set(PP_ticket['Ticket']) |\
        set(SOTON_ticket['Ticket']) | set(STON_ticket['Ticket']) |\
        set(LINE_ticket['Ticket']) | set(FC_ticket['Ticket']) |\
        set(W_ticket['Ticket']) | set(C_ticket['Ticket']) |\
        set(SC_ticket['Ticket']) | set(SO_ticket['Ticket']) |\
        set(other_ticket['Ticket'])
set(num_alpha_ticket['Ticket']) - new_set

これで計算結果が空のセットになることを確認します。

グラフを見ると、チケットによって生存率には大きな差が出ていることがわかります。

チケットのラベリング

この結果をもとにして、チケットのラベリングを行います。

number_ticket.loc[number_ticket['Ticket'] <= 100000, 'Ticket'] = 14
number_ticket.loc[(number_ticket['Ticket'] > 100000) & (number_ticket['Ticket'] <= 200000), 'Ticket'] = 15
number_ticket.loc[(number_ticket['Ticket'] > 200000) & (number_ticket['Ticket'] <= 300000), 'Ticket'] = 13
number_ticket.loc[(number_ticket['Ticket'] > 300000) & (number_ticket['Ticket'] <= 400000), 'Ticket'] = 5
number_ticket.loc[number_ticket['Ticket'] > 3000000, 'Ticket'] = 6
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('A.+'), 'Ticket'] = "1"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('C\.*A\.*.+'), 'Ticket'] = "8"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('PC.+'), 'Ticket'] = "16"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('PP.+'), 'Ticket'] = "18"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('SOTON.+'), 'Ticket'] = "3"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('STON.+'), 'Ticket'] = "11"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('LINE.*'), 'Ticket'] = "7"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('F\.C\.(C\.)*.+'), 'Ticket'] = "17"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('W.+'), 'Ticket'] = "4"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('C.+'), 'Ticket'] = "9"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('S(\.)*C.+'), 'Ticket'] = "12"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('S(\.)*O.+'), 'Ticket'] = "2"
num_alpha_ticket.loc[num_alpha_ticket['Ticket'].str.match('[^\d](Fa)*(P/PP)*(S\.P)*(S\.*W)*.+'), 'Ticket'] = "10"

num_alpha_ticket['Ticket'] = num_alpha_ticket['Ticket'].apply(lambda x: int(x))
train = pd.concat([number_ticket, num_alpha_ticket])

ここまでの処理の結果

ここまでの処理で、各変数の相関係数がどのように変化したか見てみます。

plt.figure(figsize=(10, 8))
sns.heatmap(train.corr(), annot=True, cmap='Reds')
plt.show()

f:id:pyhaya:20181122001403p:plain

TicketとSurvivedに比較的強い相関が出ました。

次回は、これらのデータを使って実際に機械学習をやってみたいと思います。

Kaggleで勝つデータ分析の技術

作者: 門脇大輔,阪田隆司,保坂桂佑,平松雄司
出版社/メーカー: 技術評論社
発売日: 2019/10/09
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

2018-11-25

機械学習を原理から理解する　線形分類

Python データサイエンス機械学習プログラミング

最近、機械学習がブームでPythonを使えばだれでも簡単に学習器を作れるようになってきましたね。Pythonはライブラリが充実しているのでモデルについて何も知らなくでも機械学習をできます。私も別に仕事で機械学習を使っているわけではないのでそのような状態に甘んじていたのですが、最近になってさすがに気持ち悪さを感じていたので勉強を始めました。

今回は簡単なモデルとして、分類問題、特に線形の二値分類問題を考えます。

対象とする問題
学習アルゴリズム
どのように解くか
Pythonで実装する

対象とする問題

仮説空間という言葉が出てくると難しく感じますが、予測に使うのは下のような関数です。

$y = sign(\mathbf{w}\cdot\mathbf{x} + b)$

$\mathbf{w}, b$ は重みとバイアスです。基本的には線形関数で、最終的にsignで符号だけ取り出すことで予測値 $y$ を算出しています。

学習アルゴリズム

与えられている特徴量を $\mathbf{x}$ 、正解ラベルを $t$ とします。この時、予測が当たっている状況を数式であらわすと、

$t = sign(\mathbf{w}\cdot\mathbf{x} + b)$

符号関数は、少し抽象的です。もう少し扱いやすい形に書き換えましょう。要は両辺で符号さえ合っていればよいので、

$t(\mathbf{w}\cdot\mathbf{x} + b) > 0$

としてもよいでしょう。訓練データが全部で $n$ 個あるような状況を考えると、重みパラメータとバイアスが満たすべき条件は、

$t_i(\mathbf{w}\cdot\mathbf{x}_i + b_i) > 0\ \ \ \ (i=1,2,\cdots n)$

となります。さらに条件を詰めます。まず、バイアスを重みパラメータの中に取り込んでしまいます。

$t_i(\mathbf{w}\cdot\mathbf{x}_i) > 0\ \ \ \ (\mathbf{w}=(w_1, w_2, \cdots, b), \mathbf{x}_i=(x_{i1}, x_{i2}, \cdots, 1))$

次に重みパラメータを $t(\mathbf{w}\cdot\mathbf{x})$ の最小値 $\gamma$ で規格化(?)します。

$\displaystyle \bar{w}=\frac{w}{\gamma}$

これをつかうことで、条件はもう少し厳しくすることができて、

$t_i(\mathbf{\bar{w}}\cdot\mathbf{x}_i) = t_i(\mathbf{w}\cdot\mathbf{x}_i)\times\frac{1}{\gamma} \ge 1$

これが求めるべきパラメータの満たすべき条件です。

どのように解くか

問題はこれをどう解くかです。これはよく見ると、次のような問題と同じであることがわかります。

maximize 0
s. t. $t_i(\mathbf{w}\cdot\mathbf{x}_i)\ge 1$

線形計画問題です。今回は目的関数はどうでもよくて、制約条件のみが問題になります。この問題の解き方は探せば見つかって、シンプレックス法(単体法)というものが有名です。

Pythonで実装する

では、Pythonで実装します。線形計画法のところはめんどくさくなってライブラリ使いました。ごめんなさい。

import numpy as np 
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split

if __name__ == '__main__':
    #サンプル生成
    X, y = make_classification(
            n_samples=500,
            n_classes=2,
            n_features=2,
            n_redundant=0,
            class_sep=3,
            )

    y = list(map(lambda x: -1 if x==0 else 1, y))
    X_train, X_test, y_train, y_test = train_test_split(X, y)

分類サンプルは、Scikit-learnのmake_classificationを使って生成しました。今回は簡単のためにサンプル数は500個、クラス数は2(二値分類)、特徴量は2種類で重要性が少ないものは０個としました。

学習アルゴリズムの本体は下のように定義します。

import pulp

def solve(X, y):
    lp = pulp.LpProblem('lp', pulp.LpMaximize)    # 解く問題を作る
    w1 = pulp.LpVariable('w1', 0)    #重みパラメータ1
    w2 = pulp.LpVariable('w2', 0)    #重みパラメータ2
    w3 = pulp.LpVariable('b', 0)    #バイアス

    lp += 0    #目的関数
    for i in range(len(X)):
        lp += y[i] * (X[i, 0] * w1 + X[i, 1] * w2 + w3) >= 1    #制約条件

    lp.solve()    #解く
    return w1.value(), w2.value(), w3.value()    #各パラメータを返す

pulpという線形計画問題を解くためのライブラリがありますのでありがたく使わせてもらいます。

学習がうまくいっているか確かめるために、テストデータを使って精度の確認を行います。

w1, w2, b = solve(X, y)   
acc = 0
for i in range(len(X_test)):
    pred = X_test[i].dot(np.array([[w1], [w2]])) + b
    if np.sign(pred) == np.sign(y_test[i]):
        acc += 1

print(acc/len(X_test))

乱数のシードを指定していないので指向のたびに値は変わりますが、おおむね9割程度の精度は出ています。

今回は、非常に単純なモデルについて書きました。その結果、構造は簡単でも9割程度の精度が出るということが確認できました(class_sep大きくしているのでもう少し精度出てもよいと思うが...)。

2018-11-24

ABC012 B 入浴時間　を解いた

プログラミング競技プログラミング

今回は、AtCoder Beginners Contest 012 のB問題を解きましたのでまとめておきます。この問題は特別アルゴリズム等が必要なわけではなく、難しくもないのですが、ゼロ埋めが必要で、私がこれをよく忘れるので、備忘録的な感じで書きました。
beta.atcoder.jp

問題文

問題は下のようになっています。

高橋君は、お風呂で湯船に浸かった秒数を数える習慣があります。
今日は、高橋君は湯船でN秒まで数えました。
しかし、秒だと解りにくいので、何時間何分何秒、という形に直したいです。
秒数Nが与えられるので、hh:mm:ss の形式に変換しなさい。
入力は以下の形式で標準入力から与えられる。
N
1行目には、高橋君が湯船に浸かった秒数を表す整数N(0≦N≦86399)が与えられる。
出力
高橋君が湯船に浸かっていた時間を、hh:mm:ssの形式で、1行で出力せよ。出力の末尾には改行をいれること。

解答

算数的な感じです。まず時間から求めて、次に分、秒と求めていけばよいです。解答はゼロ埋め出ないとだめなので、iosとiomanipをインクルードしておきます。

#include <iostream>
#include <ios>
#include <iomanip>
using namespace std;

int main() {
	int n; cin >> n;
	int hour, min, sec;

	hour = n / 3600;
	n -= hour * 3600;
	min = n / 60;
	n -= min * 60;
	sec = n;

	cout << setfill('0') << right << setw(2) << hour << ":";
	cout << setfill('0') << right << setw(2) << min << ":";
	cout << setfill('0') << right << setw(2) << sec << endl;
}

一応解説をしておくと、setfillで何で埋めるか（今回は0）を指定していて、表示するものを左右どちらに寄せるかを指定しているのが次のrightの部分、そして埋めた後に最終的に何文字にするのかを指定しているのがsetwになります。なのでsetw(4)としたときには、hour=3の時、表示は「0003」と4桁になります。