機械学習を原理から理解する 回帰
機械学習をただ使うだけでなく、どのような原理で動いているのか理解するために数学的な観点からちゃんとアルゴリズムを見てみます。
前回は線形回帰の記事を書きました。
pyhaya.hatenablog.com
今回は、前回の線形回帰のアルゴリズムを拡張して、高次の回帰をしていきます。
前回の復習(線形回帰)
前回はデータ点を直線で回帰するために、最小二乗法を使った方法について説明しました。ここでは回帰直線を
というように重みパラメータとデータ
の内積で表現しました。そして、適切な重みを見つけるための指針として正解
との二乗誤差
を最小にしようということになり、行列計算によってこのような重みパラメータを得られることを見ました。
高次多項式での回帰
前回の記事だけでも、複数の特徴量の線形和の形での回帰は可能です。今回はさらにバリエーションを増やすために高次多項式での回帰を行います。つまり、回帰曲線は下のような式であらわされます。
見やすさのため変数は1つのものを書いています。また、いつも通りバイアスは重みパラメータ内部に入れています。
理論
実は、理論的にはこの回帰は線形回帰と同一の方法で実行することができます。というのも、(3)式はベクトルの形式で書き直すと
ここでは
です。最後の1はバイアスを重みパラメータの中に取り込んだために出てきた項です。この形は線形回帰でやったものと全く同じです。なので同じアルゴリズムで解くことができます。
添え字は訓練データの番号です。
実装(Python3)
上の理論を見ながらPythonで実装を行ってみます。
import matplotlib.pyplot as plt import numpy as np from sklearn.model_selection import train_test_split from sklearn.datasets import make_regression def Regression(X, y, dim): d = X.shape[1] + 1 A = np.zeros((d+dim-1, d+dim-1)) b = np.zeros((d+dim-1, 1)) for i in range(len(X)): x = [] for j in range(1, dim+1): x += list(X[i]**j) x.append(1) x = np.array(x).reshape((d+dim-1, 1)) A += x.dot(x.T) b += y[i] * x return np.linalg.inv(A).dot(b) if __name__ == "__main__": X, y = make_regression( n_samples=50, n_features=1, noise=4, random_state=42 ) dim = 2 #何次の多項式で回帰を行うか pred = Regression(X, y, dim) x = np.linspace(-2, 1.9, 50) y_pred = np.zeros_like(x) for i in range(0, dim): y_pred += pred[i][0] * x**(i+1) y_pred += pred[dim][0] plt.figure() plt.plot(X, y, 'o') plt.plot(x, y_pred) plt.show()
回帰結果を見てみる
回帰結果を次数を変えてみてみます。まずは二次の場合フィッティング結果は下のようになります。
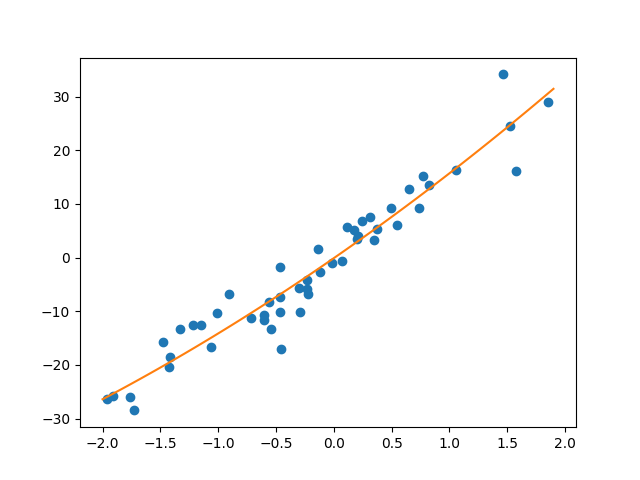
回帰はうまくいっている印象です。次に次数を増やしてみます。十次のとき
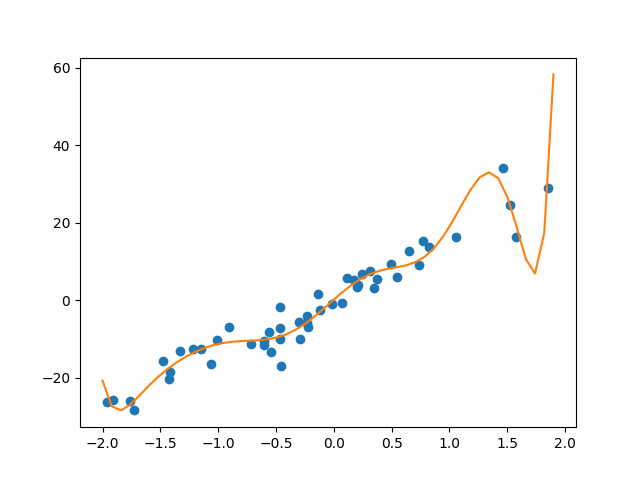
明らかにノイズも拾って回帰してしまっています。これは訓練データを過度に学習してしまっている状況で、過学習状態となっています。